CONECTORES METÁLICOS PARA VIGAS DE MADERA

La sección crítica de las columnas que soportan armaduras existe habitualmente donde se conectan las rodillas de la armadura a la columna. Cuando no se utilizan rodillas, o la columna soporta una viga, entonces se debe proveer una conexión rígida.

Las figuras figuras a continuación muestran las conexiones típicas de vigas a columnas. Ver dibujos a, b y c.

Dibujo a. EMPALME DE COLUMNA CON EL TIRANTE DE UNA CERCHA

Dibujo b. DETALLE DE EMPALME DE COLUMNA CON TIRANTE DE CERCHA

 c. CONECCIONES TÍPICAS DE TRABES Y VIGAS DE MADERA A COLUMNAS

CUBIERTAS:

ARMADURAS Y JABALCONADOS:

Considerando que la carga vertical que actúa en un nudo central es P, (ver figura 60a y 60b), el esfuerzo S que se presenta en los pares y el empuje H que tiene que ser contrarrestado por la viga tendrá un valor de:

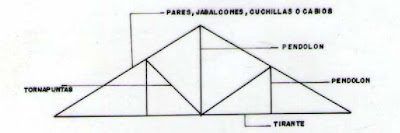
a. ARMADURA O JABALCONADO Y SUS PRINCIPALES COMPONENTES

  DIBUJO b 

DIBUJO c

  

DIBUJO b y c, EL ESFUERZO S QUE SE PRESENTA EN LOS PARES Y EL EMPUJE H QUE TIENE QUE SER CONTRARRESTADO POR LA VIGA

S =        P____                 H =        P____

         2 Sen alfa                         2 Tang alfa

Para hallar el momento de flexión de la viga así como el esfuerzo en los pendolones Z, se procede de la siguiente forma:

a) La carga que actúa sobre la viga debe ser uniformemente repartida.

b) La carga que actúa debe ser concentrada en el punto C o C´.

Caso (a)

CARGA UNIFORMEMENTE REPARTIDA A LO LARGO DE LA VIGA A-B:

En este tema la carga uniformemente repartida, que simboliza Q está constituida por la carga accidental C y el peso propio P, que está representado por la siguiente ecuación:

Q = C + P

El pendolón Z estará sometido a un esfuerzo de tracción y el valor máximo de la carga P en el punto C tendrá un valor representado en la siguiente ecuación:

P = Z = 5/8 Q.L

Y el momento máximo de la viga en el punto C, se establece por medio de la siguiente fórmula:

Mo = Q.L(al cuadrado)

                     32

Caso (b):

CARGA CONCENTRADA F EN EL PUNTO C O C':

En este condición el valor máximo de la carga P en el punto C estará dado por la fórmula:

P = Z = F

En esta situación el pendolón está sometido a tracción.

El momento de la carga en el punto C es M = 0

Cuando la carga actúa en el punto C´, el valor máximo de la carga P en este punto esta expresado en las siguientes igualdades:

P = F    Z = 0  M = 0

Otro procedimiento para la deducción de armaduras en madera es el que sigue: dibujo consecutivo.

 MÉTODO PARA CALCULAR UNA ARMADURA

Una selección de sección que generalmente es beneficioso, es la que aísla a una junta con solo dos esfuerzos desconocidos.

Como los esfuerzos y las cargas en la junta tienen que estar en equilibrio teórica y realmente, si sumamos las componentes horizontales de las fuerzas deben por obligación dar cero, por consiguiente, también la suma de las fuerzas verticales deben ser iguales a cero.

Sabemos que se conocen las líneas de acción de las fuerzas y que los esfuerzos actúan a lo largo de los ejes longitudinales de los elementos de la armadura, con esta forma se pueden deducir dos magnitudes desconocidas de dos esfuerzos de cada junta. Ver dibujos: A, B, C, D y E.

LÍNEAS DE ACCIÓN DE TODAS LAS FUERZAS

Para aplicarlo a la unión número (1) de la armadura, lo primero que se tiene que hacer es igualar a cero la suma de las componentes verticales.

Esta igualdad muestra que la componente vertical del cordón debe ser igual y opuesto a la reacción, que es de 120 kilogramos. Por consiguiente, el esfuerzo en el cordón superior en ésta unión tiene que ser una compresión igual a la mostrada en el dibujo siguiente, que es de 200 kilogramos. Después se iguala a cero la suma de las componentes horizontales. Esta igualdad indica que el esfuerzo en el cordón inferior en la unión debe ser igual y opuesto a las componentes horizontales del cordón superior.

Por consiguiente, el esfuerzo en el cordón inferior debe ser una tensión igual a la mostrada en dibujo sucesivo, que es de 160 kilogramos. Al tomar una sección alrededor de la junta numero 2, se deja  ver que el esfuerzo en la vertical es cero, conviniendo que no hay cargas en la junta y el cordón inferior es perpendicular a la vertical. Aun más, los esfuerzos deben ser los mismos en los elementos del cordón inferior en la junta, porque la suma de las componentes horizontales debe ser de cero.

Después de deducir las uniones  1 y 2 una sección alrededor de la junta numero 3 solo corta dos esfuerzos desconocidos, SBH en el cordón BH superior y SHG en la diagonal HG.

La aplicación de las leyes del equilibrio en este junta producen dos ecuaciones. Ver plano cartesiano . Dibujo a.

DIBUJO a

1-Sumatoria Fy = FAY – 80 - BHy + HGy = 0

2-Sumatoria Fx = FAx – BHx – HGx = 0

Sen de 36^o – 52´ - 12” = FAy/FA

FAy = Sen de 36^o – 52´ - 12” x FA

Sen de 36^o – 52´ - 12” = HGy/HG

HGy = Sen de 36^o – 52´ - 12” x HG

Sen de 36^o – 52´ - 12” = BHy/BH

BHy = Sen de 36^o – 52´ - 12” x BH

Cos de 36^o – 52´ - 12” = FAx/FA

FAx = Cos de 36^o – 52´ - 12” x FA

Cos de 36^o – 52´ - 12” = HGy/HG

HGx = Cos de 36^o – 52´ - 12” x HG

Cos de 36^o – 52´ - 12” = BHx/BH

BHx = Cos de 36^o – 52´ - 12” x BH

Sumatoria Fy =

FAy = 0.6 FA

HGy = 0.6 HG

BHy = 0.6 BH

Sumatoria Fx =

FAx = 0.8 FA

HGx = 0.8 HG

BHx = 0.8 BH

Estos resultados se sustituyen en las formulaciones uno y dos

1-Sumatoria Fy = 0.6FA – 80Kg – 0.6BH +0.6HGy = 0

2-Sumatoria Fx = 0.8FA – 0.8BH – 0.8HG = 0

Se admite que ambos esfuerzos desconocidos son de compresión, es decir, actúan hacia la unión.

El esfuerzo en la vertical no sale en estas igualdades pues anteriormente se determino que es cero.

El esfuerzo FA se encontró que era de 200 kilogramos de acuerdo con el análisis realizado anteriormente a la unión 1.

La solución simultánea de las dos igualdades da como resultado lo siguiente:

1)120Kg – 80Kg – 0.6BH +0.6HGy = 0 (0.8)

2)160Kg - 0.8FA – 0.8BH – 0.8HG = 0 (0.6)

1)96Kg – 64Kg – 0.48BH + 0.48HG = 0

2)96Kg        -        0.48BH – 0.48HG = 0

De la igualdad 1:

192Kg – 64 Kg – 96BH = 0

128Kg – 0.96BH = 0

128Kg /0.96 = BH

133.33Kg = BH

De la igualdad 2:

160Kg – 0.8BH – 0.8HG = 0

160Kg -0.8(133.33) - 0.8HG = 0

160Kg – 106.666 = 0.8HG

53.336Kg/0.8 = HG

66.675Kg = HG

67Kg = HG

Ahora en el siguiente paso hagamos uso de la unión número 5 para buscar el esfuerzo en el pendolón HJ. En esta unión podemos observar que el pendolón ejerce una fuerza hacia arriba en sentido contrario a la carga que le es aplicada, por esta razón en dicha unión tiene que haber la misma fuerza pero actuando en sentido contrario, lo que nos indica que es hacia arriba. Podemos ver el dibujo del plano cartesiano. Dibujo b.

EG = 160Kg

EG = EK

Sen de 36^o -  52´ - 12” = JKy/JK

JKy = Sen de 36^o -  52´ - 12” x JK

Sen de 36^o -  52´ - 12” = HGy/HG

HGy = Sen de 36^o -  52´ - 12” x HG

Cos de 36^o -  52´ - 12” = JKx/JK

JKx = Sen de 36^o -  52´ - 12” x JK

Sen de 36^o -  52´ - 12” = HGx/HG

HGx = Sen de 36^o -  52´ - 12” x HG

1-Sumatoria Fx = HGx – JKx + EK – EG = 0

2-Sumatoria Fy = HJy – JKy – HGy = 0

Ahora Sustituimos en las anteriores igualdades:

Sumatoria de Fx = 0

Cos de 36^o -  52´ - 12” x 67 – Cos 36^o -  52´ - 12” x JK = 0

0.8 x 67Kg – 0.8 x JK = 0

53.6Kg = 0.8 x JK

53.6Kg/0.8 = JK

67Kg = JK

Sumatoria Fy = 0

HJ - Sen de 36^o -  52´ - 12” x 67Kg – Sen de 36^o -  52´ - 12” x 67Kg = 0

HJ – 0.6 x 67Kg – 0.6 x 67Kg = 0

HJ – 40.2Kg – 40.2Kg = 0

HJ – 80.4Kg = 0

HJ = 80.4Kg

De tal manera que los esfuerzos que soporta la armadura quedan repartidos así:

FA = 200Kg

FE = 160Kg

BH = 133.33Kg

HG = 67Kg

HJ = 80.4Kg

Como el lado derecho es simétrico, tendrá las mismas cuantías.

Con los resultados anteriores y los esfuerzos representados en la cercha se sustituyen los resultados encontrados; en las formulas dadas para compresión :

S = F/Tc     S = KF/Tc    e = L/i

 i = Raíz cuadrada de I/S       I = b(d)al cubo/12

y   K = Para los L/i = 100 .......  K = 1/1.046 – 0.00693L/i

K Para L/i  >  100 .......... K = 1/3.525(L)al cuadrado/i

Así mismo se sustituyen los resultados para las cargas de tensión utilizando la formula            S = F/Tc sin contener el coeficiente K.

Si se quiere examinar la deformación unitaria en el caso del esfuerzo de tensión se puede emplear la expresión:  e = PL/A.E.

En la que:

E = Modulo de elasticidad de la madera.

Dichos valores también se pueden hallar buscando en las tablas de compresión admisible para piezas de sección cuadrada y las tablas de cálculo de vigas de madera sometidas a esfuerzos de flexión, vistas en anterior artículo sobre el tema, para el caso de los esfuerzos de flexión; se encuentran deduciendo previamente el Momento Máximo  Mo en Kg/cm y el Momento Resistente Wo = Mo/Tf en cm al cubo.

Para los esfuerzos de tracción emplear las tablas siguientes.

La cubierta está formada de la cercha y el material de techar, el papel de la armadura es la de sostener los materiales de cubierta.

Las armaduras de madera son utilizadas usualmente en edificios destinados a viviendas o pequeñas industrias  y las ventajas que tienen estos elementos son su peso liviano, lo económicas que son y su sencilla ejecución. Pero también tienen inconvenientes como su limitada resistencia, su continuo mantenimiento y el peligro de incendio.